顺序查找
存储结构为顺序存储或链接存储的线性表
查找的时间复杂度为 $O(N)$
二分查找
元素必须是有序的
每次将目标值与中间节点的值进行比较,再判断其落入中间节点的左侧或右侧。
可以使用迭代或递归实现。
插值查找
二分查找进阶
联系查字典,将二分查找中的 $mid = \frac{low + high}{2}$ 修改为自适应的 $mid = low + (key - a[low]) / a[high] - a[low]) * (high -low)$ 及将二分查找中的比例 0.5 改为自适应的值,根据关键字在表中的位置,让下一次查找更靠近关键字,从而减少了查找的次数。
插值查找一般适用于表长较大,同时关键字分布较为均匀的表。
复杂度:$O(log_2(log_2n))$
斐波那契查找
类比二分查找,当表长等于某斐波那契数时使用。
最坏情况时间复杂度为 $O(log_2n)$,期望复杂度 $O(log_2n)$
二叉树查找
二叉搜索树的特点是左子节点小于父节点,父节点小于右子节点。
此方案的查找效率较高,但是需要维护二叉树,并且在查找树严重不平衡时退化为“链表”。
将二叉搜索树进行优化,可以参考平衡二叉树、红黑树。
平衡查找树
2-3 Tree
每个节点保存1个或2个值(对应可以拥有2个或3个子节点)
性质:在一个完全平衡的2-3查找树中,根节点到每一个叶节点的距离都相同。
红黑树
红黑树的思想是对2-3查找树进行编码,特别是对其中的3-node节点添加额外的信息。
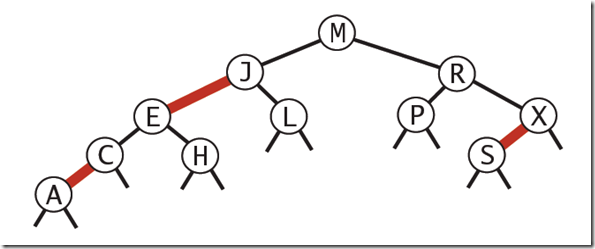
可以想像两个红色边链接的节点对应2-3查找树中的3-node。
红黑树的定义:
- 红色节点向左倾斜;
- 一个节点不可能有两个红色连接;
- 根节点到每个叶节点的黑色链接个数相同。
红黑树的应用:
- Java:
Java.util.TreeMap,Java.util.TreeSet; - C++:
STL::map,STL::multimap,STL::multiset; - .NET:
SortedDictionary,SortedSet
B树
B树可以看作是2-3查找树的拓展,其每个节点允许有M-1个子节点
B树的定义
- 根节点至少有两个子节点
- 每个节点有M-1个key,并以升序排列
- 其他节点至少有 M/2 个子节点
基本操作演示动画:

B树的优点:
- 每一个节点包含 key 和 value, 因此经常访问的元素可能距离根节点更近,可以更快访问。
B+树
B+树的定义
- 有 k 个子节点的节点必然有 k 个关键码
- 非叶节点仅具有索引作用
- 叶节点存放记录相关的信息
- 树的所有叶节点构成一个有序链表,可以按照关键码排序的次序遍历全部记录
试想一下,在文件系统中,若该文件在磁盘上的分区恰好不属于同一个父节点,此时B+树与B树的性能差异
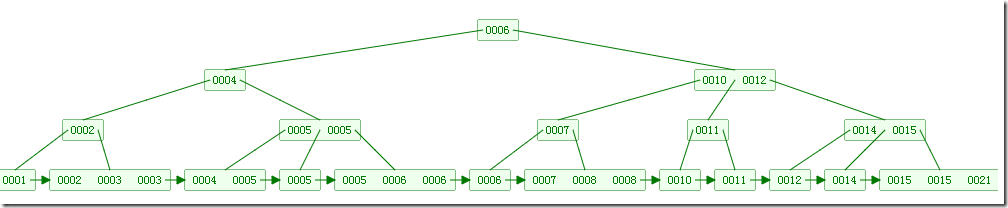
如下为B+树的操作动画:

B+树的优点:
- 内部节点不含数据信息,内存页可以存放更多的key。
- 数据存放紧密,具有更好的空间局部性,访问叶节点关联的数据具有更高的缓存命中率。
- 叶节点构成有序链表,对整棵树的遍历更快。
- 便于区间查找与搜索。(非同父节点时优势明显)
B树/B+树的应用:
- Windows: HPFS
- Mac: HFS, HFS+
- Linux: ResiserFS, XFX, Ext3FS, JFS
- 数据库: ORACLE, MySQL, SQLServer
分块查找
每一块中数据不必有序。 但快间数据有序。 (类比快排的中间步骤)
算法步骤:
- 选取各块中的最大关键字构成索引表
- 二分查找确定索引块
- 索引块内顺序查找目标值
哈希查找
哈希函数:使关键字分散到指定大小的顺序结构的转换关系。
算法流程:
- 使用哈希函数构造哈希表
- 解决地址冲突
- 拉链法
- 线性探测法
- 执行哈希查找