Divide and Conquer
基本思想
Divide-and-conquer:
Break up problem into several parts.
Solve each part recursively.
Combine solutions to sub-problems into overall solution.
Most common usage.
- Break up problem of size n into two equal parts of size ½ n.
- Solve two parts recursively.
- Combine two solutions into overall solution in linear time.
Consequence.
- Brute force: $n^2$.
- Divide-and-conquer: $n log n$.
Mergesort
- Divide array into two halves.
- Recursively sort each half.
- Merge two halves to make sorted whole.
Challenge for the bored. In-place merge. [Kronrud, 1969]
using only a constant amount of extra storage
Def. T(n) = number of comparisons to mergesort an input of size n.
Mergesort recurrence:$$\begin{equation}T(n)=\left{\begin{array}{lr}\text{0,}&\quad\text{if n = 1,}\T(\lceil \frac{n}{2}) + T(\lfloor \frac{n}{2} \rfloor) + n, &\quad\text{otherwise.}\end{array}\right.\end{equation}$$$T(n) = O(n log_2n). $
Counting Inversions
计算逆序对可在归并排序的基础上完成
Divide-and-conquer.
Divide: separate list into two pieces.
Conquer: recursively count inversions in each half.
Combine: count inversions where $a_i$ and $a_j$ are in different halves, and return sum of three quantities
$$\begin{align*}&Sort-and-Count(L)\quad{ &\qquad\text{if list L has one element}&\qquad\qquad \text{return 0 and the list L}&\qquad \text{Divide the list into two halves A and B}&\qquad (r_A, A) \leftarrow Sort-and-Count(A)&\qquad (r_B, B) \leftarrow Sort-and-Count(B)&\qquad (r_B, L) \leftarrow Merge-and-Count(A, B)}\end{align*}$$
Closest Pair of Points
【鸽巢原理】【分治】
Closest pair: Given n points in the plane, find a pair with smallest Euclidean distance between them
Algorithm:
- Divide: draw vertical line L so that roughly ½ n points on each side.
- Conquer: find closest pair in each side recursively
- Combine: find closest pair with one point in each side.【利用鸽巢原理剪枝,减少需要判断的数量】
- Return best of 3 solutions.
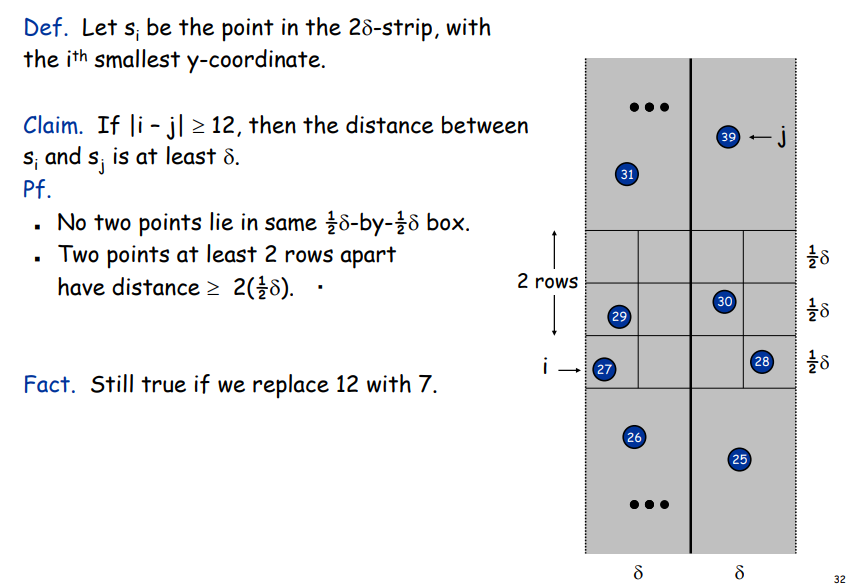
优化 combine 步骤:
Find closest pair with one point in each side, assuming that $distance < \delta = min{左右两个部分的最近点}$.
- So, only need to consider points within $\delta$ of line L
鸽巢原理可知,最多check6个点

Running Time$$\begin{align*}T(n) &\leq 2T(\frac{n}{2}) + O(nlogn)&=O(nlog^2n)\end{align*}$$More optimal:
- Don't sort points in strip from scratch each time.
- Each recursive returns two lists: all points sorted by y coordinate,and all points sorted by x coordinate.
- Sort by merging two pre-sorted lists.
$$\begin{align*}T(n) &\leq 2T(\frac{n}{2}) + O(n)&=O(nlogn)\end{align*}$$
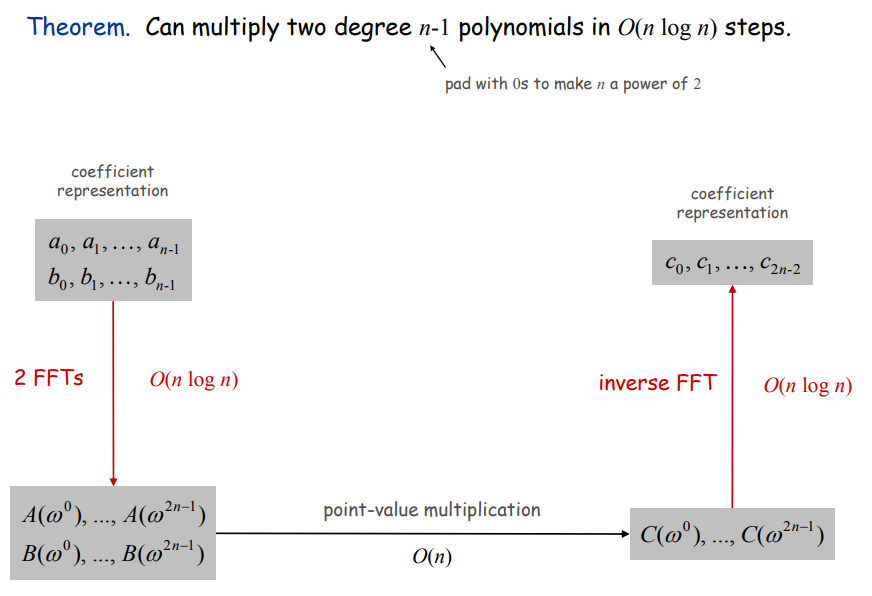
Multiply
Convolution and FFT
FFT: Fast way to convert between time-domain and frequency-domain.
Alternate viewpoint. Fast way to multiply and evaluate polynomials.
coefficient representation
Polynomial.$$A(x) = a_0 + a_1x + a_2x^2 + \dots + a_{n-1}x^{n-1}\B(x) = b_0 + b_1x + b_2x^2 + \dots + b_{n-1}x^{n-1}$$Add. $O(n)$ arithmetic operations.$$A(x) + B(x) = (a_0+b_0) + (a_1 + b_1)x + \dots + (a_{n-1} + b_{n-1})x^{n-1}$$Evaluate. $O(n)$ using Horner's method.$$A(x) = a_0 + x(a_1 + x(a_2 + \dots + x(a_{n-2} + x(a_{n-1}))\dots))$$Multiply (convolve): $O(n^2)$ using brute force$$A(x) \times B(x) = \sum_{i=0}^{2n-2}c_ix^i,\qquad where, c_i = \sum_{j=0}^{i}a_jb_{i-j}$$
Point-Value Representation
Fundamental theorem of algebra. [Gauss, PhD thesis]
A degree n polynomial with complex coefficients has exactly n complex roots.Corollary. A degree n-1 polynomial A(x) is uniquely specified by its evaluation at n distinct values of x.
Polynomial:$$A(x): (x_0, y_0), \dots , (x_{n-1}, y_{n-1})\B(x): (x_0, z_0), \dots , (x_{n-1}, z_{n-1})$$Add: $O(n)$ arithmetic operations.$$A(x) + B(x): (x_0, y_0 + z_0), \dots , (x_{n-1}, y_{n-1} + z_{n-1})$$Evaluate: $O(n^2)$ using Lagrange's formula.$$A(x) = \sum_{k=0}^{n-1}y_k\frac{\prod_{j \neq k}(x-x_j)}{\prod_{j\neq k}(x_k - x_j)}$$Multiply (convolve). $O(n)$, but need 2n-1 points$$A(x) \times B(x): (x_0, y_0 \times z_0), \dots , (x_{n-1}, y_{n-1} \times z_{n-1})$$
Converting Between Two Representations
Coefficient => point-value: $O(n^2)$ for matrix-vector multiply (or $O(n)$ Horner's).Point-value => coefficient: $O(n^3)$ for Gaussian elimination.
Improve? => Divide and conquer
Divide. Break polynomial up into even and odd powers$$\begin{align*}A(x) &= a_0 + a_1x + a_2x^2 + a_3x^3 + a_4x^4 + a_5x^5 + a_6x^6 + a_7x^7\A_{even}(x) &= a_0 + a_2x^2 + a_4x^4 + a_6x^6\A_{odd}(x) &= a_1x + a_3x^3 + a_5x^5 + a_7x^7\A(x) &= A_{even}(x^2) + x A_{odd}(x^2)\A(-x) &= A_{even}(x^2) - x A_{odd}(x^2)\end{align*}$$Intuition: Choose four complex points to be ±1, ±i.$$\begin{align*}A(1) &= A_{even}(1) + A_{odd}(1)\A(-1) &= A_{even}(1) - A_{odd}(1)\A(i) &= A_{even}(-1) + i A_{odd}(-1)\A(-i) &= A_{even}(-1) - i A_{odd}(-1).\end{align*}$$
Can evaluate polynomial of degree $\leq$ n at 4 points by evaluating two polynomials of degree $\leq \frac{2}{n}$ at 2 points.
Fast Fourier Transform (FFT)
Roots of Unity:
- Def: An $n_{th}$ root of unity is a complex number x such that $x_n$ = 1.
- Fact. The $n_{th}$ roots of unity are: $\omega_0, \omega_1, \dots , \omega_{n-1}$ where $\omega = e^{\frac{2\pi i}{n}}$
- Pf. $(\omega^k)^n = (e^{2\pi i k /n} ) ^n = (e^{\pi i}) ^{2k} = (-1)^{2k} = 1$
- Fact. The $\frac{n}{2}_{th}$ roots of unity are: $v^0, v^1, \dots, v^{n/2-1}$ where $v = \omega^2 = e^{4\pi i / n}$.
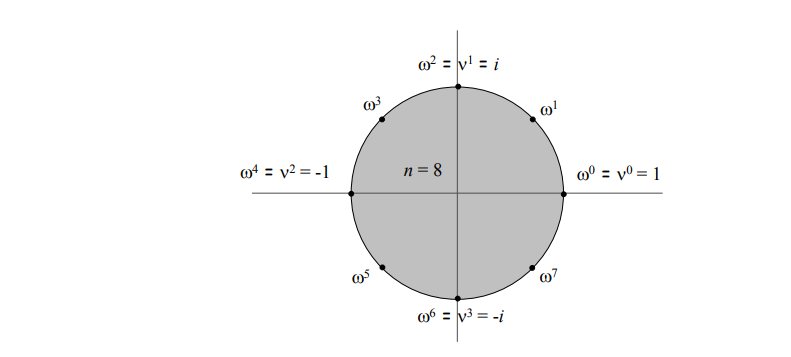
Goal. Evaluate a degree n-1 polynomial $A(x) = a_0 + a_1x + a_2x^2 + \dots + a_{n-1}x^{n-1}$ at its $n_{th}$ roots of unity: $\omega_0, \omega_1, \dots , \omega_{n-1}$
Divide: Break up polynomial into even and odd powers.$$\begin{align*}A_{even}(x) &= a_0 + a_2x^1 + a_4x^2 + \dots + a_{n-2}x^{n/2-2}\A_{odd}(x) &= a_1x + a_3x^1 + a_5x^2 + \dots + a_{n-1}x^{n/2-1}\A(x) &= A_{even}(x^2) + x A_{odd}(x^2)\end{align*}$$Conquer: Evaluate $A_{even}(x)$ and $A_{odd}(x)$ at the $\frac{n}{2}_{th}$ roots of unity: $v^0, v^1, \dots, v^{n/2-1}$.
Combine:
- $A(\omega^k) \qquad= A_{even}(v^k) + \omega^kA_{odd}(v^k), \qquad 0 \leq k \leq n/2$
- $A(\omega^{k+1/2n}) = A_{even}(v^k) - \omega^kA_{odd}(v^k), \qquad 0 \leq k \leq n/2$

Running Time:$$\begin{align*}T(n) &= 2T(\frac{n}{2}) + \Theta(n) &= \Theta(nlogn)\end{align*}$$

Summary